由 Venkatesh Rajagopalan（数据科学与分析总监）、Mahadevan Balasubramaniam（首席数据科学家）和 Arun Subramaniyan（BHGE Digital 的数据科学与分析副总裁）发布

我们相信乔治·博克斯（George Box）著名评论的略微修改版本：“所有模型都是错误的，有些是有用的” 在很短的时间内。无论模型有多么复杂，它都需要定期更新以准确地反映底层系统。在该博客系列的 第一 部分和 第二 部分中，我们介绍了构建融合物理学的混合概率模型的理念，以预测稀疏数据集中的复杂非线性现象。特别是在第二部分中，我们描述了如何使用新获得的信息更新概率模型。通过使用来自处于更高级退化阶段的不同但相似的物理资产的数据，我们能够对物理系统如何随时间退化的已知未知行为进行建模。

在本系列的最后一部分，我们将描述被称为“未知未知”的不确定性以及用于有效建模它们的技术。为了在一个应用程序中将我们建模理念的所有方面整合在一起，我们将预测锂离子电池在不知道其实际退化特征时的性能。

电池健康模型

电池存储已成为从消费类设备到电动汽车等各种应用的关键。特别是锂离子电池由于其高功率和能量密度而被广泛使用。对电池性能进行建模对于预测其荷电状态（SoC）和健康状态（SoH）至关重要。电池随着使用时间的推移，其性能会以非线性方式下降。人们进行了大量的研究来了解电池退化的现象并开发预测电池寿命的模型。有关电池退化原因及其相关建模的更多详细信息，请参阅丰富的文献[1]。

电池的两个主要指标是电池电压和容量（通常以安培小时表示）。下图描绘了放电循环中电池电压随放电电流变化的时间曲线。随着放电电流增加，电池电压随时间的推移下降得更快。

不同放电电流下的电池电压与时间的关系。

下图显示了单个电流放电（2.5 A）下电池电压随充放电循环的典型退化情况。随着循环（即使用）次数的增加，即使对于相同的电流放电，电池的电压输出能力也会下降。可以在此处找到验证这种行为的实验结果[2,3]。

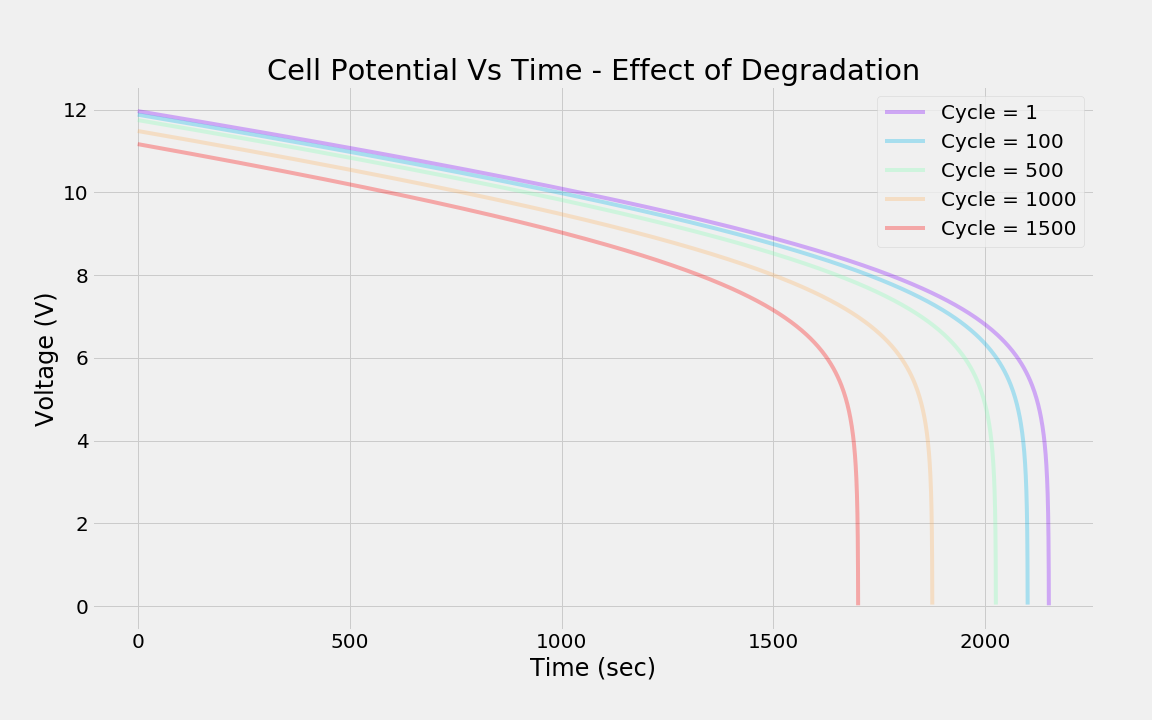循环（使用）对电池电压的影响。

虽然有几种方法可以对电池特性进行建模，包括物理模型和混合模型，但我们打算说明一种数据驱动的策略，用于估计电池的健康状态（或退化），而无需了解退化的物理机制。这种方法的主要优点是，该模型只需要来自原始（几乎没有或没有退化）电池的数据，并且退化的程度可以简单地作为异常（即与标称行为的偏差）来跟踪，以便进行早期检测。此外，该模型可以利用测量值进行持续更新 - 对于准确预测电池电压至关重要。这种持续模型更新是必需的，因为每个客户对资产的操作都是独一无二的。我们将这种更新称为“个性化模型”，其中我们可以持续更新模型以跟踪特定客户在现场的使用情况。挑战在于以计算效率高的方式使用零星的、有噪声的现场测量值来执行这种更新。

数据生成

我们将使用以下公式生成放电曲线

V= a-0.0005*Q + log(b-Q) 其中 a=4–0.25*I 且 b=6000–250*I

其中 a 是线性下降部分，b 是渐近下降部分，如放电曲线所示。

I 是放电电流，Q 表示电池消耗的电量，其中
a 和 b 的值是名义上的，代表放电曲线轮廓[4]。

每个应用都是独一无二的，并且对电池的使用方式也不同。考虑两个变化维度：放电量和放电速率。然后，考虑这两个维度也可以应用于充电循环。换句话说，电池可以完全或部分放电和充电；它也可以缓慢或快速地放电和充电。每个电池的使用情况和制造过程中的差异会影响每个电池的退化方式。我们通过为退化参数 δ 选择一个随机值并计算随机循环下随机使用情况下的响应来模拟这种差异。经过多次充放电循环后，电池性能会下降，电压和总容量会降低。为了用一个简单的例子说明退化跟踪的概念，我们将通过功能性地改变整个循环中电池的线性部分和渐近部分来模拟退化。

如果 δ 是退化因子，那么修改后的电池响应将是：

来自退化电池的数据用于模型更新，而不是用于构建初始模型。请注意，这种函数形式只是一个近似，但仍然代表了电池现场行为。

已知未知与未知未知：使用上述数据集，此问题可以归类为已知未知情况或未知未知情况。如果建模者知道描述退化现象的物理方程，从而了解退化参数 (δ) 与物理方程的具体交互方式，那么这个问题可以解决为已知未知情况。了解这些具体细节后，建模者可以将其归类为模型更新问题，如我们博客系列的 第二 部分所述。

但是，如果底层物理机制未知，那么建模者别无选择，只能使用来自原始电池的“原始”数据来构建数据驱动的模型，然后随着模型性能下降而更新数据驱动的模型。在不知道具体退化机制的情况下，建模者可能别无选择，只能更新数据驱动模型的很大一部分。希望模型中具有足够的自由度，并且新数据集中的信息量足以准确地更新模型。在解决未知未知的现实世界应用中，这些条件很常见。

我们将在此展示后一种对未知未知进行建模的情况，方法是使用来自原始电池的数据构建 DNN 模型。我们提供了代表性值以确保读者可以创建数据以构建“通用”深度学习模型。

我们将遵循的博客剩余部分的流程如下所示：

用于说明未知未知的建模过程。

下面所示的简单 DNN 模型架构具有 5 个隐藏层（4,16, 64,16,4），将用于说明这些概念。

用于模拟电池性能的简单深度神经网络架构。

使用最多 200 个 epochs 训练 DNN 会产生一个足够准确的模型，如下所示。原始电池的训练点和测试点都被合理地预测。

DNN 模型的训练和测试预测结果。

我们将向原始电池添加非线性退化，如上所述。退化电池性能的具体示例由下图中的蓝色点表示，对应于 0.163 的退化参数 (δ)。根据实际使用情况，蓝色点表示电池在放电循环期间的实际测量值。

原始 DNN 模型预测结果与退化电池数据相比。

添加退化几乎立即使该模型变得不准确。由于我们不知道确切的退化机制，因此我们将选择使用粒子滤波器更新最后一层隐藏层的超参数[5]。

使用粒子滤波器进行模型更新

粒子滤波 (PF) 是一种通过蒙特卡罗模拟实现递归贝叶斯滤波器的技术。其关键思想是用一组具有相关权重的随机样本表示后验密度函数；我们根据这些样本和权重计算估计值。随着样本数量变得非常大，PF 估计值将接近最佳贝叶斯估计值。有关各种 PF 算法的详细讨论，请参阅此 教程。

与我们之前的 博客文章 中描述的无迹卡尔曼滤波器 (UKF) 方法一样，我们将 PF 的“状态”建模为随机游走过程。输出模型是 DNN。描述过程模型和测量模型的公式总结如下

x[k] = x[k-1] + w[k]
y[k] = h(x[k], u[k]) + v[k]

其中

• x 表示 PF 的状态（即需要更新的 DNN 的超参数）
  
• h 是 DNN 的函数形式
  
• u 表示 DNN 的输入：电流和容量
  
• y 是 DNN 的输出：电池电压
  
• w 表示过程噪声
  
• v 表示测量噪声
  

PF 算法除了过程和测量模型中噪声样本的独立性外，没有其他假设。粒子滤波器对于使用现场测量更新 DNN 模型来说是稳健的，并且足够通用，可以用于模型训练。有关详细讨论，请参阅这篇 论文。下面总结了基于 PF 的模型更新方法的主要步骤。

1. 从建议的密度（称为重要性密度）生成初始粒子。
   
2. 为粒子分配权重，并对权重进行归一化。
   
3. 为每个粒子添加过程噪声。
   
4. 为所有粒子生成输出预测。
   
5. 计算每个粒子的实际输出值和预测输出值之间的误差似然。
   
6. 使用粒子的误差似然更新粒子权重。
   
7. 对权重进行归一化。
   
8. 计算样本的有效数量。
   
9. 如果有效样本数量 < 阈值，则对粒子进行重采样。
10. 估计状态向量及其协方差。
    
11. 对每个测量重复步骤 3 到 10。
    

基于 PF 的更新 DNN 模型的方法已作为 Depend On Docker 项目实现，可以在这个 仓库 中找到，以及这个 Google Colab 中找到。如前所述，PF 仅假设过程和测量模型中的噪声是独立的。因此，与 UKF 假设相比，我们不需要假设噪声服从高斯分布。因此，TensorFlow Probability 的 tfp.distributions 模块提供的广泛功能可用于实现粒子滤波器中的所有关键步骤，包括

• 生成粒子，
  
• 生成噪声值，以及
  
• 计算给定状态的观察似然。
  

下面提供了一些算法步骤的代码片段。

生成初始粒子集

粒子滤波器使用 TF Probability 生成的粒子集进行初始化。

import tensorflow as tf
import tensorflow_probability as tfp
tfd = tfp.distributions

# Generate Particles with initial state vector pf['state'] and state covariance matrix pf['state_cov']
sess = tf.Session()
state = np.array(pf['state'])
state.shape = (num_st, )                                  # num_st is the number of state variables
mvn = tfd.MultivariateNormalFullCovariance(loc=state, covariance_matrix=pf['state_cov'])
particles = sess.run(mvn.sample(pf['Ns']))                # pf['Ns'] is the number of particles to be generated

为每个粒子生成输出

通过将粒子值设置为 DNN 最后一层的偏差和权重并运行模型，为每个粒子生成输出预测。

def pf_predout(coef, loc_pm, p_ampDraw, time_val, tVarDict):
    
    p_ampSec = p_ampDraw * time_val
    baseW_Out = tVarDict['W_OUT:0']
    n_dim = len(coef)

    coef = np.array(coef)
    coef.shape = (n_dim,)
    
    tVarDict['b_OUT:0'] = [coef[0]]
    for idxW in np.arange(len(baseW_Out)):
        baseW_Out[idxW, 0] = coef[idxW + 1]
    tVarDict['W_OUT:0'] = baseW_Out

    yhat = np.asmatrix(loc_pm.predictSingleRowAugmented(p_ampDraw, p_ampSec, tVarDict))

    return yhat

更新每个粒子的权重

生成预测后，计算粒子处于真实状态的似然，并相应地更新与该粒子关联的权重。

def update_weights(y, yhat, R, prev_weight): 
    from scipy.stats import norm
    
    likelihood = norm.pdf(y-yhat, 0, R)
    updt_weight = prev_weight * likelihood
    
    return updt_weight

对粒子进行重采样

如果需要，通过系统重采样对粒子进行重采样。

def systematic_resample(sess, weights):
    N = len(weights)

    # make N subdivisions and choose positions with a random offset
    positions = (sess.run(tf.random.uniform((1, ))) + np.arange(N)) / N

    indexes = np.zeros(N, 'i')
    cum_sum = np.cumsum(weights)
    i, j = 0, 0
    while i < N:
        if positions[i] < cum_sum[j]:
            indexes[i] = j
            i = i + 1
        else:
            j = j + 1
    return indexes
  
  def resample_from_index(particles, weights, indexes):
    particles = particles[:, indexes]
    weights = weights[indexes]
    weights.fill(1.0 / len(weights))

    return particles, weights, indexes

结果与讨论

使用粒子滤波器更新基线 DNN 模型最后一层的权重和偏差，使用第一个数据点，会产生下面用绿色显示的模型预测。阴影区域表示使用 500 个随机粒子计算的预测不确定性。

更新后的模型预测（来自第一个更新点）。

该算法将下一个更新点选择为观察结果超出预测不确定性的时间。在本例中，它是时间点 13（接近 700 秒）。只要观察到的数据超出模型预测的不确定性，就逐步更新模型，从而产生如下一所示的期望精度。

基于预测不确定性启动的顺序模型更新结果。

将所有模型组合在一起，我们得到整个退化周期的预测。很明显，基线模型完全错过了退化，导致电池循环结束时电压预测出现 50% 的误差。因此，使用预测不确定性进行简单更新使建模者能够解释“未知的未知”。

最终模型（仅最新更新）预测与初始模型的比较。

模型预测误差的比较。

对于四个节点的最后一个隐藏层，我们下面描述了电池模型的初始状态和最终更新后的状态。显然，状态发生了显著变化，并且模型预测有所改善，即使更新仅使用了一些数据点。状态分布的变化也可以被视为系统异常（在本例中为退化 δ）的指示。因此，这些图表明数据中包含足够的信息来更新模型。相比之下，使用没有任何相关信息的数据集更新模型将导致模型继续不准确。因此，选择正确的模型更新时间与更新模型的方法一样重要，甚至更加重要。

最后一个 DNN 隐藏层参数的初始状态和最终状态的比较。

总结

在工业界实现人工智能需要结合多个学科：领域知识、概率方法、传统机器学习和深度学习。我们已经展示了有效结合这些学科来使用有限且不确定的数据对现实世界现象进行建模的技术。本系列博客的第三部分侧重于建模“未知的未知”。要构建工业资产的数字孪生，必须构建“一个”模型，该模型不断调整以跟踪每个生态系统中每个“资产”随时间的现场测量。基于原始数据构建的 DNN 层的权重和偏差更新的粒子滤波方法可用于构建“一个”模型。在现实世界的工业应用中，许多挑战限制了有用数据的数量，包括噪声、缺失值和不一致的测量。因此，选择建模内容、选择合适的建模方法（物理、数据驱动或混合）以及选择哪些参数需要持续更新对于维护有用的模型至关重要。

致谢

这篇博客是 Google 和 BHGE 多个团队辛勤工作和深度合作的结果。我们特别感谢 Mike Shwe、Josh Dillon、Scott Fitzharris、Alex Walker、Fabio Nonato 和 Gautam Subbarao 的多次编辑、结果、代码片段，以及最重要的热烈支持。