作者：Ian Fischer、Alex Alemi、Joshua V. Dillon 和 TFP 团队


在 2019 年的 TensorFlow 开发者峰会上，我们 宣布 了 TensorFlow Probability (TFP) 层。在演示中，我们展示了如何在极少的代码行中构建一个强大的回归模型。这里，我们将展示使用 TFP 层构建变分自编码器 (VAE) 的简单性。

TensorFlow Probability 层

TFP 层提供了一个高级 API，用于使用 Keras 将分布与深度网络组合在一起。此 API 使构建结合深度学习和概率编程的模型变得容易。例如，我们可以使用深度网络的输出参数化概率分布。我们将在本文中使用这种方法。

变分自编码器和 ELBO

变分 自编码器 (VAE) 是流行的生成模型，被用于许多不同的领域，包括 协同过滤、图像压缩、强化学习 以及 音乐 和 草图 的生成。

在 VAE 的传统推导中，我们想象一些生成数据的过程，例如潜在变量生成模型。考虑绘制数字的过程，例如在 MNIST 中。假设在你绘制数字之前，你首先决定要绘制哪个数字，并在脑海中想象一些模糊的图片。然后，你拿起笔，试图在现实世界中创造出你脑海中的图片。我们可以将这个两步过程形式化

1. 你从某个先验分布 z ~ p(z) 中采样一些潜在表示 z。这就是你脑海中的模糊图片——比如一个“3”。
2. 根据你的样本，你绘制实际的图片表示 x，它本身被建模为一个随机过程 x ~ p(x|z)。这体现了每次你写“3”时，它至少看起来有点不同的想法。

因此，当创建手写数字时，我们想象某些变异是由于该过程固有的某种信号造成的，例如 MNIST 数字的类别标识，而某些变异是由于噪声造成的，例如同一个人绘制的同一数字的不同样本之间的线条精确角度的差异。广义上说，VAE 试图通过对这两个过程的明确模型来尝试将信号与噪声分离。

为了训练这个目标，我们最大化 ELBO（证据下界）目标

其中三个概率密度函数是

• p(z)，潜在表示 z 的先验分布，
• q(z|x)，变分编码器，以及
• p(x|z)，解码器——给定潜在表示 z，图像 x 的可能性有多大。

ELBO 是log p(x) 的下界，即观察到的数据点的对数概率。ELBO 方程中的第一个积分是重建项。它询问我们从图像 x 开始、将其编码为 z、将其解码并得到原始 x 的可能性有多大。第二项是KL 散度 项。它衡量编码器和先验分布之间的接近程度；你可以将此项视为试图使编码器保持诚实。如果编码器生成的 z 样本在给定先验分布的情况下太不可能，则目标比生成更典型的 z 样本（更接近先验分布）要差。因此，编码器应该只在这样做带来的成本超过重建项带来的收益时才与先验分布有所不同。

代码

从上面的描述中，我们可以看到，分别对三个不同的组件进行建模是自然而然的：先验 p(z)、变分编码器 q(z|x) 和解码器 p(x|z)。你可以通过运行 这个 colab 来进行操作，该 colab 在几分钟内就可以在云 GPU 上训练 MNIST 上的 VAE。

先验

VAE 中最常用的简单先验分布是各向同性的高斯分布

tfd = tfp.distributions
encoded_size = 16
prior = tfd.Independent(tfd.Normal(loc=tf.zeros(encoded_size), scale=1),
                        reinterpreted_batch_ndims=1)

在这里，我们只创建了一个 TFP 独立高斯分布，没有学习参数，并且我们指定了我们的潜在变量 z 将具有 16 维。

编码器

对于我们的编码器分布，我们将使用一个完全协方差的高斯分布，其均值和协方差矩阵由神经网络的输出参数化。这听起来可能很复杂，但使用 TFP 层表示起来非常容易

tfpl = tfp.layers
encoder = tfk.Sequential([
    tfkl.InputLayer(input_shape=input_shape),
    tfkl.Lambda(lambda x: tf.cast(x, tf.float32) - 0.5),
    tfkl.Conv2D(base_depth, 5, strides=1,
                padding='same', activation=tf.nn.leaky_relu),
    tfkl.Conv2D(base_depth, 5, strides=2,
                padding='same', activation=tf.nn.leaky_relu),
    tfkl.Conv2D(2 * base_depth, 5, strides=1,
                padding='same', activation=tf.nn.leaky_relu),
    tfkl.Conv2D(2 * base_depth, 5, strides=2,
                padding='same', activation=tf.nn.leaky_relu),
    tfkl.Conv2D(4 * encoded_size, 7, strides=1,
                padding='valid', activation=tf.nn.leaky_relu),
    tfkl.Flatten(),
    tfkl.Dense(tfpl.MultivariateNormalTriL.params_size(encoded_size),
               activation=None),
    tfpl.MultivariateNormalTriL(
        encoded_size,
        activity_regularizer=tfpl.KLDivergenceRegularizer(prior, weight=1.0)),
])

编码器只是一个普通的 Keras Sequential 模型，由卷积和密集层组成，但输出传递给 TFP 层 MultivariateNormalTril()，该层透明地将来自最终 Dense() 层的激活拆分为指定均值和（下三角）协方差矩阵（多元正态分布的参数）所需的各个部分。我们使用了一个助手 tfpl.MultivariateNormalTriL.params_size(encoded_size)，使 Dense() 层输出正确的激活数量（即分布的参数）。最后，我们说这个分布应该对最终损失贡献一个“正则化”项。具体来说，我们将编码器和先验分布之间的 KL 散度添加到损失中，这是我们上面描述的 ELBO 中的KL 项。（有趣的事实：我们可以通过将 weight 参数更改为 1 以外的值，简单地将这个 VAE 转换为 β-VAE！）

解码器

对于我们的解码器，我们将使用一个简单的“平均场解码器”，在本例中将是一个像素独立的伯努利分布

decoder = tfk.Sequential([
    tfkl.InputLayer(input_shape=[encoded_size]),
    tfkl.Reshape([1, 1, encoded_size]),
    tfkl.Conv2DTranspose(2 * base_depth, 7, strides=1,
                         padding='valid', activation=tf.nn.leaky_relu),
    tfkl.Conv2DTranspose(2 * base_depth, 5, strides=1,
                         padding='same', activation=tf.nn.leaky_relu),
    tfkl.Conv2DTranspose(2 * base_depth, 5, strides=2,
                         padding='same', activation=tf.nn.leaky_relu),
    tfkl.Conv2DTranspose(base_depth, 5, strides=1,
                         padding='same', activation=tf.nn.leaky_relu),
    tfkl.Conv2DTranspose(base_depth, 5, strides=2,
                         padding='same', activation=tf.nn.leaky_relu),
    tfkl.Conv2DTranspose(base_depth, 5, strides=1,
                         padding='same', activation=tf.nn.leaky_relu),
    tfkl.Conv2D(filters=1, kernel_size=5, strides=1,
                padding='same', activation=None),
    tfkl.Flatten(),
    tfpl.IndependentBernoulli(input_shape, tfd.Bernoulli.logits),
])

这里形式与编码器基本相同，但现在我们使用转置卷积将我们的潜在表示（一个 16 维向量）转换为一个 28 x 28 x 1 张量。该最终张量参数化了像素独立的伯努利分布。

损失

现在，我们准备构建完整模型并指定损失函数的其余部分。

vae = tfk.Model(inputs=encoder.inputs,
                outputs=decoder(encoder.outputs[0]))

我们的模型只是一个 Keras 模型，其中输出被定义为编码器和解码器的组合。由于编码器已经将 KL 项添加到损失中，因此我们只需要指定重建损失（上面 ELBO 的第一项）。

negative_log_likelihood = lambda x, rv_x: -rv_x.log_prob(x)

vae.compile(optimizer=tf.optimizers.Adam(learning_rate=1e-3),
            loss=negative_log_likelihood)

损失函数接受两个参数——原始输入 x 和模型的输出。我们将其称为 rv_x，因为它是一个随机变量。此示例演示了 TFP 层的核心魔力之一——即使 Keras 和 Tensorflow 将 TFP 层视为输出张量，TFP 层实际上也是Distribution 对象。因此，我们可以使损失函数成为给定模型的数据的负对数似然：-rv_x.log_prob(x)。

等等，什么？

值得花点时间了解 TFP 层实际上在做什么，以便透明地与 Keras 集成。正如我们所说，TFP 层的输出实际上是一个 Distribution 对象。我们可以使用以下代码进行检查

x = eval_dataset.make_one_shot_iterator().get_next()[0][:10]
xhat = vae(x)
assert isinstance(xhat, tfd.Distribution)

但是，如果 TFP 层返回一个 Distribution，那么当我们将解码器与编码器的输出组合时会发生什么：decoder_model(encoder_model.outputs[0]))？为了使 Keras 将编码器分布视为一个张量，TFP 层实际上会将分布“具体化”为来自该分布的一个样本，这只是一个花哨的说法，意思是 Keras 将 Distribution 对象视为我们本来会得到的张量，如果我们调用了 encoder_model.sample()。但是，当我们需要直接访问 Distribution 对象时，我们可以——就像我们在损失函数中调用 rv_x.log_prob(x) 时一样。TFP 层自动提供分布式和张量式行为，因此你无需担心 Keras 会感到困惑。

训练

训练模型与训练任何 Keras 模型一样容易：我们只需调用 vae_model.fit()

vae.fit(train_dataset,
        epochs=15,
        validation_data=eval_dataset)

使用这个模型，我们可以获得大约 115 奈特的 ELBO（奈特 是比特的自然对数等价物——115 奈特大约是 165 比特）。当然，这种性能不是最先进的，但从这个基本设置开始，很容易使三个组件中的任何一个变得更强大。此外，它已经可以生成看起来不错的数字了！

通过对来自 MNIST 测试集的图像进行编码而生成的解码器模式。

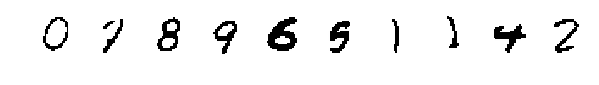通过从先验分布中采样而生成的解码器模式。

总结

在本博文中，我们展示了如何将深度学习与概率编程相结合：我们构建了一个变分自编码器，该编码器使用 TFP 层将 Keras Sequential 模型的输出传递给 TFP 中的概率分布。

我们利用了 TFP 层的张量式和分布式语义，使我们的代码相对简单。