由 Pavel Sountsov、Chris Suter、Jacob Burnim、Joshua V. Dillon 和 TensorFlow Probability 团队发布

背景

在 2019 年的 TensorFlow Dev Summit 上，我们宣布了 TensorFlow Probability (TFP) 中的概率层。在这里，我们将更详细地演示如何使用 TFP 层来管理回归预测中固有的不确定性。

回归和概率

回归 是机器学习从业者可以应用于预测问题的最基本的技术之一。但是，许多基于回归的分析忽略了对预测中不确定性的适当量化，这部分是由于所需复杂程度所致。为了开始量化不确定性，一个特别优雅的解决问题的方法是将回归模型写成 _P(y | x, w)_，即给定输入 ( _x_) 和一些参数 ( _w_) 的标签 (_y_) 的概率分布。我们可以通过最大化标签的概率来拟合此模型，或者等效地，最小化负对数似然损失：-log _P_(_y_ | _x_)。在 Python 中

negloglik = lambda y, p_y: -p_y.log_prob(y)

我们可以使用各种标准的连续和分类以及损失函数来使用此回归模型。例如，连续标签的均方误差损失意味着 _P_(_y_ | _x_, _w_) 是一个 正态分布，具有固定的尺度（标准差）。分类的交叉熵损失意味着 _P_(_y_ | _x_, _w_) 是 分类分布。

在这篇文章中，我们将展示如何将 TensorFlow Probability (TFP) 中的概率层与 Keras 一起使用，在这个简单的基础上进行构建，逐步推断任务中越来越多的不确定性。您可以在 Google Colab 中进行操作。

案例 1：简单线性回归

我们将从一个简单的线性回归模型开始，该模型拟合到一些数据

import tensorflow as tf
import tensorflow_probability as tfp
tfd = tfp.distributions

# Build model.
model = tf.keras.Sequential([
  tf.keras.layers.Dense(1),
  tfp.layers.DistributionLambda(lambda t: tfd.Normal(loc=t, scale=1)),
])

# Do inference.
model.compile(optimizer=tf.optimizers.Adam(learning_rate=0.05), loss=negloglik)
model.fit(x, y, epochs=500, verbose=False)

# Make predictions.
yhat = model(x_tst)

推理和预测部分应该对任何使用过 Keras 的人都很熟悉，但模型构建看起来会有所不同。我们明确说明我们正在使用以输入为中心的、尺度为 1 的正态分布对标签进行建模。tfp.layers.DistributionLambda 层实际上返回了 tfd.Distribution 的一个特殊实例（有关此内容的更多详细信息，请参见附录 A），因此我们可以自由地获取其均值并将其绘制在数据旁边

mean = yhat.mean()

因此，我们设法用标签分布的预测均值捕获了数据的总体趋势（蓝色圆圈）。但是，我们可以看到数据具有更多结构：似乎 _y_ 的可变性随着 _x_ 的增加而增加。我们目前编写的模型无法捕获此细节，但在下一节中，我们将展示如何修改模型以使其具有这种能力。

案例 2：已知未知数

在上一节中，我们已经看到对于 _x_ 的任何特定值，_y_ 都有可变性。我们可以将这种可变性视为问题本身固有的。这意味着即使我们拥有无限的训练集，我们仍然无法完美地预测标签。这种不确定性的一个常见例子是公平硬币翻转的结果（假设你没有配备详细的物理模型等）。无论我们过去看到了多少次翻转，我们都无法预测未来翻转的结果。

我们假设这种可变性与 _x_ 的值具有已知的函数关系。让我们使用与 _y_ 均值相同的线性函数来建模这种关系。

# Build model.
model = tfk.Sequential([
  tf.keras.layers.Dense(1 + 1),
  tfp.layers.DistributionLambda(
      lambda t: tfd.Normal(loc=t[..., :1],
                           scale=1e-3 + tf.math.softplus(0.05 * t[..., 1:]))),
])

# Do inference.
model.compile(optimizer=tf.optimizers.Adam(learning_rate=0.05), loss=negloglik)
model.fit(x, y, epochs=500, verbose=False)

# Make predictions.
yhat = model(x_tst)

现在，除了预测标签分布的均值之外，我们还预测其尺度（标准差）。在以相同的方式进行训练和形成预测后，我们可以对 _y_ 作为 _x_ 的函数的可变性做出有意义的预测。与之前一样

mean = yhat.mean()
stddev = yhat.stddev()
mean_plus_2_stddev = mean - 2. * stddev
mean_minus_2_stddev = mean + 2. * stddev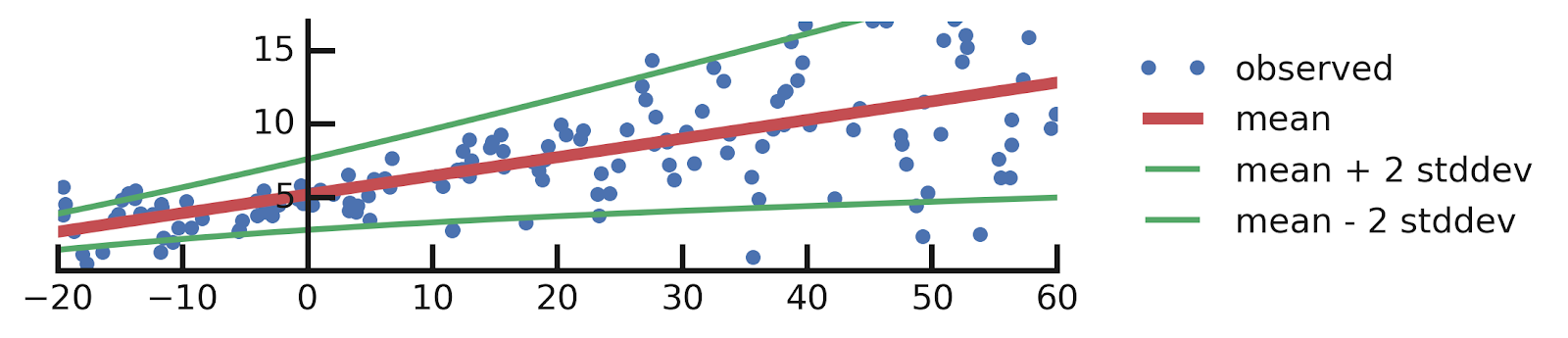

好多了！我们的模型现在对 _x_ 变得更大时 _y_ 应该是什么不太确定了。这种不确定性称为 _偶然_不确定性，因为它代表了基础过程固有的变化。虽然我们取得了进展，但偶然不确定性并不是此问题中不确定性的唯一来源。在进一步讨论之前，让我们考虑一下我们迄今为止忽略的另一个不确定性来源。

案例 3：未知未知数

数据中的噪声意味着我们无法完全确定 _x_ 和 _y_ 之间线性关系的参数。例如，我们在上一节中发现的斜率似乎是合理的，但我们并不确定，也许一个稍微平缓或陡峭的斜率也可能是合理的。这种不确定性被称为 _认知_不确定性；与偶然不确定性不同，认知不确定性可以通过获取更多数据来减少。为了了解这种不确定性，我们将用 TFP 的 DenseVariational 层替换标准 Keras Dense 层。

DenseVariational 层使用权重上的变分后验 _Q_(_w_) 来表示其值中的不确定性。该层将 _Q_(_w_) 规范化为接近 _先验_ 分布 _P_(_w_)，该分布在查看数据之前对权重中的不确定性进行建模。

对于 _Q_(_w_)，我们将使用一个以可训练对角协方差矩阵为中心的变分后验的多元正态分布。对于 _P_(_w_)，我们将使用一个具有可训练位置和固定尺度的标准多元正态分布作为先验。有关此层工作原理的更多详细信息，请参见附录 B。

让我们将所有这些放在一起

# Build model.
model = tf.keras.Sequential([
  tfp.layers.DenseVariational(1, posterior_mean_field, prior_trainable),
  tfp.layers.DistributionLambda(lambda t: tfd.Normal(loc=t, scale=1)),
])

# Do inference.
model.compile(optimizer=tf.optimizers.Adam(learning_rate=0.05), loss=negloglik)
model.fit(x, y, epochs=500, verbose=False)

# Make predictions.
yhats = [model(x_tst) for i in range(100)]

尽管涉及的算法很复杂，但使用 DenseVariational 层很简单。上面代码的一个有趣方面是，当我们使用具有这种层的模型进行预测时，每次预测都会得到不同的答案。这是因为 DenseVariational 本质上定义了一个模型集合。让我们看看这个集合告诉我们关于模型参数的信息。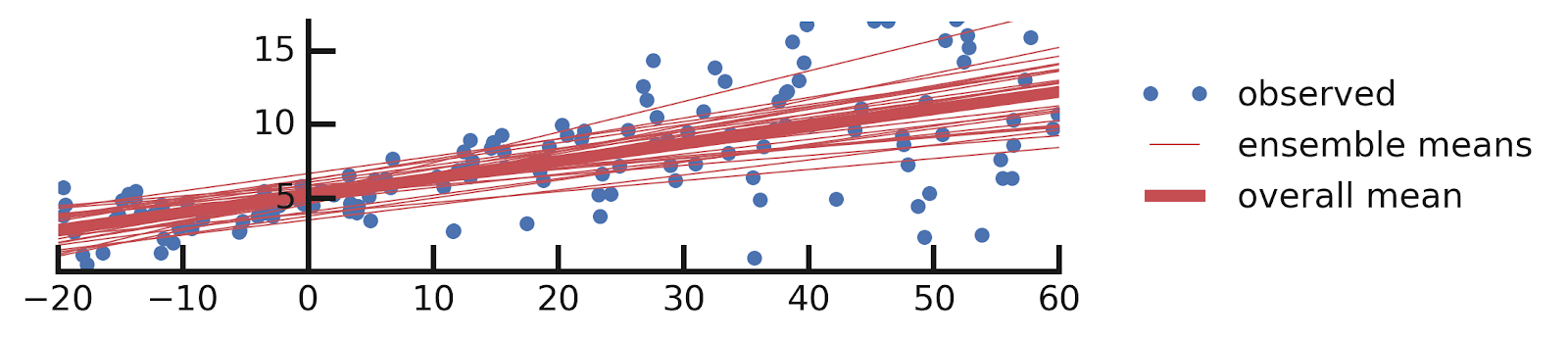

每条线代表从后验分布中随机抽取模型参数的不同结果。如我们所见，实际上关于线性关系存在相当大的不确定性。即使我们不关心 _y_ 在 _x_ 的任何特定值上的可变性，如果我们对远离 0 的 _x_ 进行预测，斜率中的不确定性也应该让我们停下来。

请注意，在此示例中，我们正在训练 _P_(_w_) 和 _Q_(_w_)。这种训练对应于使用 _经验贝叶斯_ 或 _II 型最大似然_。我们使用这种方法，这样我们就无需指定斜率和截距参数的先验位置，如果我们对问题没有先验知识，这可能很难做到。此外，如果您将先验设置得与它们的真实值相差甚远，那么后验可能会受到这种选择的不利影响。使用 II 型最大似然的缺点是，您会失去权重的一些正则化优势。如果您想对不确定性进行适当的贝叶斯处理（如果您有一些先验知识，或者更复杂的先验），您可以使用不可训练的先验（参见附录 B）。

案例 4：已知和未知未知数

现在我们已经分别查看了偶然和认知不确定性，我们可以使用 TFP 层的可组合 API 来创建一个模型，该模型报告这两种类型的不确定性

# Build model.
model = tf.keras.Sequential([
  tfp.layers.DenseVariational(1 + 1, posterior_mean_field, prior_trainable),
  tfp.layers.DistributionLambda(
      lambda t: tfd.Normal(loc=t[..., :1],
                           scale=1e-3 + tf.math.softplus(0.01 * t[..., 1:]))),
])

# Do inference.
model.compile(optimizer=tf.optimizers.Adam(learning_rate=0.05), loss=negloglik)
model.fit(x, y, epochs=500, verbose=False);

# Make predictions.
yhats = [model(x_tst) for _ in range(100)]

我们对先前模型所做的唯一更改是，我们在 DenseVariational 层添加了一个额外的输出，以对标签分布的尺度进行建模。与我们之前的解决方案一样，我们得到了一个模型集合，但这一次，它们都报告了 _y_ 作为 _x_ 的函数的可变性。让我们绘制这个集合

请注意，此模型的预测与仅考虑偶然不确定性的模型的预测之间的定性差异：该模型预测，随着 _x_ 变得更负，可变性也会增加，此外还会变得更正——这对于偶然不确定性的简单线性模型来说是不可能做到的。

结论

TFP 层背后的指导原则在于，从业者应该专注于编写模型，而不是损失。在本文中，我们一直保持用户指定的损失相同，即实现负对数似然的 negloglik 函数，同时对模型进行局部修改以处理越来越多的不确定性类型。API 还允许您自由地在最大似然学习、II 型最大似然和完全贝叶斯处理之间切换。我们相信此 API 极大地简化了概率模型的构建，并很高兴将其与世界分享。

此 API 将在下一个稳定版本 TensorFlow Probability 0.7.0 中可以使用，并且已在 nightly 版本中提供。请加入我们参加 [email protected] 论坛，了解最新的 TensorFlow Probability 公告和其他 TFP 讨论。

奖励：从零开始

到目前为止，我们一直在假设数据遵循一条直线。如果我们不知道输入和标签之间的函数关系怎么办？假设我们有一个模糊的感觉，即只有当相应的输入与我们已经观察到的输入相近时，预测的标签才应该与已看到的标签相似？换句话说，我们唯一想做出的假设是，我们拟合到数据的函数是平滑的。

在做出这些假设的同时进行回归的标准工具是 高斯过程。这个强大的模型使用核函数来编码关于输入和标签之间关系应采取的形式的平滑性假设（和其他全局函数属性）。以数据为条件，它会形成一个关于与这些假设和数据一致的 _函数_ 的概率分布。

TFP 提供了 VariationalGaussianProcess 层，它使用变分近似（类似于我们在上面情况 3 和 4 中所做的）来对完整的 Gaussian Process 进行近似，从而构建出一个高效且灵活的回归模型。为了简单起见，我们将仅考虑关于输入和标签之间关系形式的认知不确定性。在我们将要做的假设方面，我们将简单地假设我们正在拟合的函数在局部是平滑的：它可以在整个数据集上尽可能地变化，但如果两个输入彼此接近，它将返回相似的值。

num_inducing_points = 40
model = tf.keras.Sequential([
    tf.keras.layers.InputLayer(input_shape=[1], dtype=x.dtype),
    tf.keras.layers.Dense(1, kernel_initializer='ones', use_bias=False),
    tfp.layers.VariationalGaussianProcess(
        num_inducing_points=num_inducing_points,
        kernel_provider=RBFKernelFn(dtype=x.dtype),
        event_shape=[1],
        inducing_index_points_initializer=tf.constant_initializer(
            np.linspace(*x_range, num=num_inducing_points,
                        dtype=x.dtype)[..., np.newaxis]),
        unconstrained_observation_noise_variance_initializer=(
            tf.constant_initializer(
                np.log(np.expm1(1.)).astype(x.dtype))),
    ),
])

# Do inference.
batch_size = 32
loss = lambda y, rv_y: rv_y.variational_loss(
    y, kl_weight=np.array(batch_size, x.dtype) / x.shape[0])
model.compile(optimizer=tf.optimizers.Adam(learning_rate=0.01), loss=loss)
model.fit(x, y, batch_size=batch_size, epochs=1000, verbose=False)

# Make predictions.
yhats = [model(x_tst) for _ in range(100)]

由于其强大的功能，该模型的定义要复杂得多：我们需要定义一个新的损失函数，并且有更多参数需要指定。在不久的将来，TFP 团队将致力于进一步简化此模型。然而，正如结果所证明的那样，这种额外的复杂性是值得的。

VariationalGaussianProcess 已经发现了训练集中存在的周期性结构！事实上，这种结构一直存在于贯穿本文使用的数据中——你是否在模型发现它之前就注意到了？重要的是，模型是在我们没有告诉它数据中存在任何周期性的情况下发现了这种结构的。而且，正如预期的那样，它仍然为我们提供了不确定性的度量。例如，在接近 0 的地方，周期性结构并不那么明显，因此模型不会在该区域内对任何这种关系做出承诺。

附录 A：DistributionLambda 如何工作？

DistributionLambda 是一种特殊的 Keras 层，它使用 Python lambda 来构建一个以层输入为条件的分布。

layer = tfp.layers.DistributionLambda(lambda t: tfd.Normal(t, 1.))
distribution = layer(2.)
assert isinstance(distribution, tfd.Normal)
distribution.loc
# ==> 2.
distribution.stddev()
# ==> 1.

此层使我们能够像我们所做的那样编写 negloglik 损失函数，因为 Keras 将模型最后一层的输出传递给损失函数，而对于本文中的模型，所有这些层都返回分布。有关如何使用这些层的更多方法，请参见 使用 TensorFlow Probability 层构建变分自编码器 文章。

附录 B：DenseVariational 如何工作？

DenseVariational 层使用变分推断来学习其权重上的分布。这是通过最大化 ELBO（证据下界）目标来实现的。

ELBO 使用三个分布

• P(w) 是权重的先验分布。这是我们在训练模型之前假设权重遵循的分布。
• Q(w; θ) 是由参数 θ 参数化的变分后验分布。这是我们在训练完模型后对权重分布的近似值。
• P(Y | X, w) 是将所有输入 X、所有标签 Y 和权重关联起来的似然函数。当用作 Y 上的概率分布时，它指定了给定 X 和权重的 Y 的变化。

ELBO 是 log P(Y | X) 的下界，即在对权重的 uncertainty 进行边缘化后，给定输入的标签的对数似然。ELBO 通过权重先验分布（第二项）相对于 Q 的 KL 散度，与从输入预测标签的能力（第一项）进行权衡。当数据很少时，第二项占主导地位，我们的权重保持接近先验分布，作为副作用，这有助于防止过拟合。

DenseVariational 分别计算 ELBO 的两项。第一项是通过用 Q 中的单个随机样本进行近似来计算的。如果我们仔细观察该项，那么对于 w 的任何特定值，它恰好是我们一直在本文中用于回归的负对数似然损失。因此，通过简单地从 Q 中抽取一组随机权重，然后计算常规损失，我们就自动地近似了 ELBO 的第一项。

第二项是通过分析计算的，然后作为正则化损失添加到层中——类似于我们指定 L2 正则化的方式。此损失由 Keras 为我们添加到第一项中。

用于计算第一项的采样解释了我们如何能够通过多次使用相同的输入调用模型来生成多个模型：每次我们这样做时，我们都会根据 Q 分布对权重进行新的采样。

我们如何指定先验分布和变分后验分布？它们与我们在情况 2 中看到的一样，是可训练的分布。例如，我们在情况 3 中使用的可训练先验分布定义如下。

def prior_trainable(kernel_size, bias_size=0, dtype=None):
  n = kernel_size + bias_size
  return tf.keras.Sequential([
      tfp.layers.VariableLayer(n, dtype=dtype),
      tfp.layers.DistributionLambda(lambda t: tfd.Independent(
          tfd.Normal(loc=t, scale=1),
          reinterpreted_batch_ndims=1)),
  ])

它只是一个可调用函数，它返回一个带有 DistributionLambda 层的常规 Keras 模型！这里唯一的新组件是 VariableLayer，它简单地返回可训练变量的值，忽略任何输入（因为先验分布不以任何输入为条件）。请注意，如果我们想将此转换为不可训练的先验分布，我们将向 VariableLayer 构造函数传递 trainable=False。