作者：Rina Panigrahy

矩阵压缩

张量和矩阵是机器学习模型（尤其是深度网络）的基本组成部分。通常需要小型模型，以便它们可以适应手机、家用助手、汽车、恒温器等设备 - 这不仅有助于缓解网络可用性、延迟和功耗问题，而且也是最终用户的期望，因为推理的用户数据不需要离开设备，这会带来更强的隐私感。由于此类设备具有较低的存储、计算和功耗能力，为了使模型适应，通常需要缩减某些方面，例如限制词汇量大小或降低质量。为此，能够压缩模型不同层中的矩阵非常有用。有几种流行的矩阵压缩技术，例如剪枝、低秩近似、量化和随机投影。我们将论证，大多数这些方法本质上可以通过某种分解算法将矩阵分解为两个因子。

压缩方法

剪枝：一种流行的方法是剪枝，其中通过丢弃（归零）较小的条目来稀疏化矩阵 - 通常可以剪枝矩阵的大部分而不会影响其性能。

低秩近似：另一种常见的方法是低秩近似，其中将原始矩阵 A 分解为两个更薄的矩阵，方法是通过最小化Frobenius误差 |A-UV^T|_F ，其中 U、V 是低秩（例如秩 k）矩阵。可以使用SVD（奇异值分解）来获得最佳解决方案。
字典学习：低秩近似的变体是稀疏分解，其中因子是稀疏的而不是薄的（注意，薄矩阵可以看作是稀疏的特例，因为薄矩阵也类似于在不存在的列中具有零条目的更大矩阵）。稀疏分解的一种流行形式是字典学习；这对于高而薄的嵌入表很有用，因此一开始就具有低秩 - 字典学习利用了这样一个可能性，即即使嵌入条目的数量可能很大，但也可能存在较小的基本向量字典，使得每个嵌入向量都是这些字典向量中几个的稀疏组合 - 因此，它将嵌入矩阵分解为较小的字典表的乘积和一个稀疏矩阵，该矩阵指定每个嵌入条目组合了哪些字典条目。

常用的随机投影涉及使用随机投影矩阵将输入投影到更小维度的向量，然后训练更薄的矩阵，这仅仅是矩阵分解的特例，其中一个因子是随机的。

量化：另一种流行的方法是量化，其中通过可能将条目四舍五入到少量位来量化每个条目或一个条目块，以便每个条目（或一个条目块）被量化代码替换。因此，原始矩阵被分解为码本和编码表示；原始矩阵中的每个条目都是通过在码本中查找编码矩阵中的代码来获得的。因此，它可以再次被视为码本和编码矩阵的特殊乘积。码本可以通过对矩阵的条目或条目块应用某种聚类算法（例如 k 均值）来计算。这实际上是具有单一稀疏性的字典学习的特例，因为每个块都被表示为码本中的一个向量（可以看作是字典），而不是稀疏组合。剪枝也可以看作是量化的特例，其中每个条目或块都指向码本条目，该条目要么为零，要么为其本身。

因此，从剪枝到量化再到字典学习存在一个连续体，它们都是矩阵分解的形式，就像低秩近似一样。

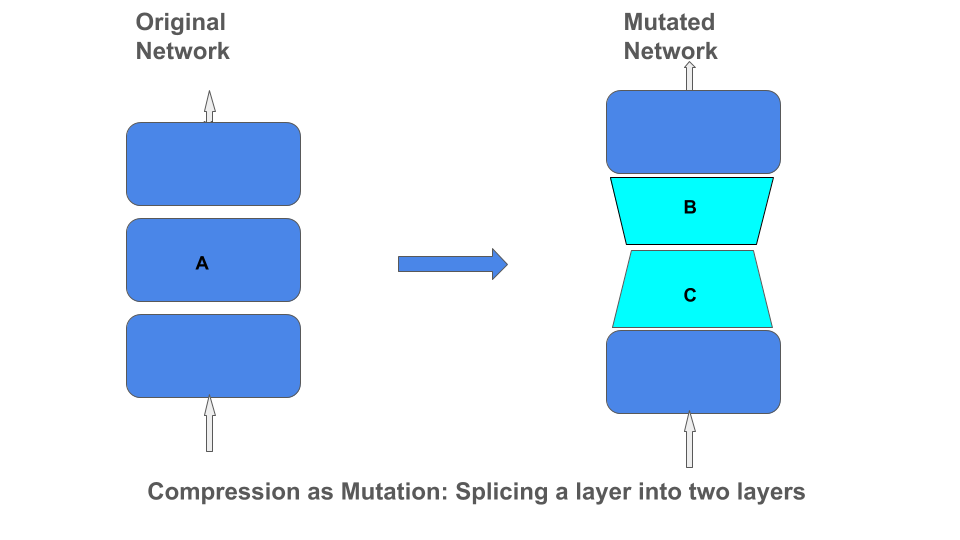
分解作为变异

将这些不同的矩阵分解类型应用于网络可以看作是通过将一层分解为两层的乘积来改变网络架构。

Tensorflow 矩阵压缩操作符

鉴于各种矩阵压缩算法，如果有一个简单的操作符可以应用于 tensorflow 矩阵以使用这些算法中的任何一个在训练期间压缩矩阵，那将很方便。这将节省先训练完整矩阵、应用分解算法创建因子，然后创建另一个模型来可能重新训练因子的开销。例如，对于剪枝，一旦确定了掩码矩阵 M，人们可能仍然希望继续训练未掩码的条目。类似地，在字典学习中，人们可能希望继续训练字典矩阵。

我们已经开源了这样一个压缩操作符，它可以接受在特定 MatrixCompressor 类中指定的任何自定义矩阵分解方法。然后，要应用某种压缩方法，只需调用 apply_compression(M, compressor = myCustomFactorization) 即可。该操作符动态地将单个矩阵 A 替换为通过指定自定义分解算法分解 A 而获得的两个矩阵 B*C 的乘积。该操作符实时地让矩阵 A 训练一段时间，并在某个训练快照中应用分解算法，并将 A 替换为因子 B*C，然后继续训练因子（乘积 ' * ' 不一定是标准矩阵乘法，而是可以是压缩类中指定的任何自定义方法）。压缩操作符可以接受前面提到的任何几种分解方法。

对于字典学习方法，我们甚至有一个基于 OMP 的字典学习实现，它比 scikit 实现更快。我们还有一种改进的基于梯度的剪枝方法，该方法不仅考虑了条目的幅度来决定要剪枝哪些条目，而且还通过测量损失相对于条目的梯度来考虑它对最终损失的影响。

因此，我们正在实时地对网络进行变异，在开始时只有一组矩阵，最终在该层中产生两组矩阵。我们的分解方法甚至不需要基于梯度，而是可以涉及更多离散风格的算法，例如散列、OMP 用于字典学习，或聚类用于 k 均值。因此，我们的操作符表明，可以将基于连续梯度的​​方法与更传统的离散算法混合。实验还包括一种基于随机投影的方法，称为simhash - 要压缩的矩阵乘以一个随机投影矩阵，并且条目四舍五入为二进制值 - 因此，它是一个随机投影矩阵和一个二进制矩阵的分解。以下图表显示了这些算法在压缩CIFAR10 和PTB 模型方面的性能。结果表明，虽然低秩近似在 CIFAR10 上优于 simhash 和 k 均值，但在 PTB 上字典学习略好于低秩近似。

CIFAR10

PTB

结论

我们开发了一个操作符，它可以接受任何以分解形式给出的矩阵压缩函数，并创建一个 tensorflow API 以在训练期间动态地将该压缩应用于任何 tensorflow 变量。我们通过几个不同的分解算法（包括字典学习）展示了它的使用，并在 CIFAR10 和 PTB 的模型上展示了实验结果。这也展示了如何将离散过程（例如稀疏矩阵分解和 k 均值聚类）与连续过程（例如梯度下降）动态地结合起来。

致谢

这项工作得益于许多人的贡献，包括 Xin Wang、Badih Ghazi、Khoa Trinh、Yang Yang、Sudeshna Roy 和 Lucine Oganesian。同时感谢 Zoya Svitkina 和 Suyog Gupta 的帮助。