作者：Venkatesh Rajagopalan，数据科学与分析总监，以及 Arun Subramaniyan，BHGE Digital 数据科学与分析副总裁

在本系列的第一篇博文中，我们介绍了我们的分析理念，即结合领域知识、概率方法、传统机器学习 (ML) 和深度学习技术来解决工业界中最棘手的问题。我们还通过构建用于裂纹扩展的混合模型的例子说明了这种方法。我们与 TensorFlow Probability (TFP) 团队和 Google 的云 ML 团队持续合作，加速了我们大规模开发和部署这些技术的进程。以前难以解决的问题现在可以通过将物理知识与看似无关的技术结合起来，并利用现代、可扩展的软件和硬件来解决。

在本博文中，我们将展示我们的分析方法的另一个应用 - 使用新获得的信息更新现有模型。我们将使用《工程系统预测和健康管理：入门》一书中提供的相同裂纹扩展示例。

更新模型的必要性

预测模型旨在预测系统的未来状态。这些预测模型可以完全基于数据驱动，也可以基于系统的已知物理特性，或者可以是混合模型 - 数据和物理特性的结合。在工业界，这些模型用于估计组件（例如，涡轮机叶片）或系统（例如，潜水电机）的剩余使用寿命。这些模型可以使用现实世界的现场数据（如果可用）或来自模拟或受控实验的数据来开发。

从模拟或受控实验中开发的模型需要用现场数据验证和改进（如果可用）。然而，在现场数据可用后仅使用现场数据重建模型通常不可行，因为在给定时间内通常可用现场数据的数量非常有限。此外，通常需要保留模型“内核”，仅修改其系数。因此，需要一种方法，允许持续更新模型以提高其准确性。

我们将考虑以下场景：基于物理知识和已知材料特性构建了用于裂纹扩展的初始模型，正如我们在第一篇博文中所做的那样。当使用该模型预测裂纹尺寸时，模型预测在初始阶段相当准确，但随着时间的推移，在预测和观测之间观察到了显著差异。

因此，利用新获得的裂纹测量值来更新现有模型，使其更加准确将非常有用。这种场景在工业领域非常常见；当改变材料特性或在组件（例如，燃气轮机叶片）中引入新设计时，将不会有现场数据可用。本文讨论了一种基于无迹卡尔曼滤波器 (UKF) 的方法来更新初始裂纹扩展模型。

关于数据的简要讨论

下面展示了《工程系统预测和健康管理：入门》一书中提供的包含裂纹测量值和循环的数据集。

尽管此数据来自教科书中的示例，但它展示了在现场数据中通常观察到的某些特征，例如以下特征

1. 噪声

虽然裂纹尺寸相对于循环的总体趋势是增加的，但它不是严格的单调的。在某些情况下，观察到的裂纹小于先前时刻的测量值。这很可能是由于测量误差，这是现场数据中常见的特征。换句话说，数据是有噪声的。

2. 小样本量

数据集仅包含 16 个数据点，不足以构建任何有意义的数据驱动模型。因此，利用对裂纹扩展物理特性的理解来构建有用的模型至关重要。

为了使事情更加复杂，在现实世界的应用中，甚至可能无法从同一个组件或系统获取累积退化的数据。用于建模的可用数据通常来自不同资产，它们处于不同程度的退化阶段。因此，混合建模方法对于工业分析至关重要。

为了说明更新模型的方法，将数据集分为三部分

• 初始数据集 - 初始模型预测在这个数据集中相当准确。它包含前六个数据点 [循环 0 到 500]。
  
• 更新数据集 - 初始模型预测在这个数据集中不准确。顾名思义，此数据集用于更新初始模型。它包含接下来的五个数据点 [循环 600 到 1000]。
  
• 测试数据集 - 此数据集用于验证更新模型的预测。它包含最后五个数据点 [循环 1100 到 1500]
  

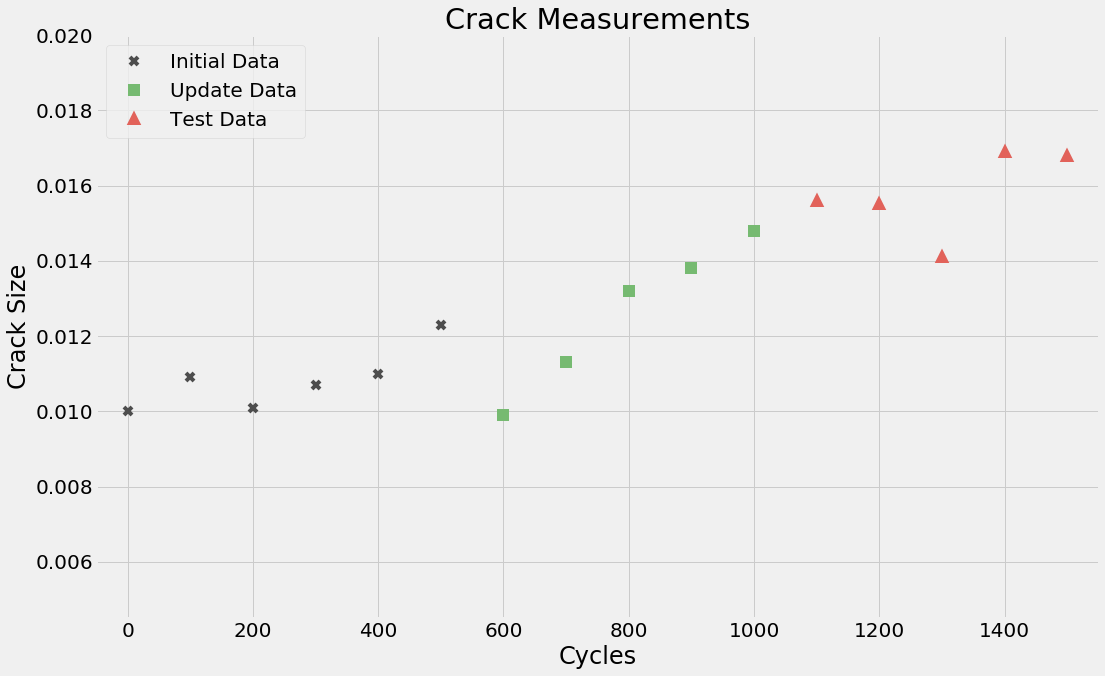
使用最小二乘最小化获得的初始模型参数为 logC = -22.135 & m = 3.765，其中 C 和 m 是材料特性。初始数据集的模型预测如下所示： 与测量值相比，模型预测相当准确。初始数据集的均方误差 (MSE) 发现为：MSE(i)=3.93 10^-7。该模型对对应于更新数据集的时间段内的裂纹尺寸的预测如下所示。 很明显，初始模型的预测不再准确。更新数据点的 MSE 变为 MSE(u)=5.67 10^-6，几乎是初始误差 MSE(i) 的 14 倍！此外，随着循环次数的增加，模型预测和观察到的裂纹尺寸在更新数据集中存在明显的差异。因此，需要改进模型以提高其准确性。

更新方法

可以使用的一种模型更新技术是 卡尔曼滤波器 (KF) 及其变体，即 扩展卡尔曼滤波器 (EKF) 和 无迹卡尔曼滤波器 (UKF)。在 KF 的情况下，做出以下假设

1. 过程模型是线性的
   
2. 测量模型是线性的
   
3. 初始状态是高斯分布的
   

EKF 和 UKF 允许放宽前两个假设。卡尔曼滤波器执行的一个核心操作是将高斯随机变量 (GRV) 通过系统动力学传播。在 EKF 中，状态分布由 GRV 近似，然后通过非线性系统的二阶线性化进行解析传播。这种传播会在转换后的 GRV 的真实后验均值和协方差中引入较大的误差，这可能导致滤波器性能欠佳，有时还会导致滤波器发散。

UKF 通过使用确定性采样方法解决了这个问题。状态分布再次由 GRV 近似，但现在使用一组精心选择的样本点（称为 sigma 点）来表示。当 sigma 点通过非线性系统传播时，它们能够 准确地捕获到三阶（泰勒级数展开）的任何非线性的后验均值和协方差。相比之下，EKF 只能实现一阶精度。值得注意的是，UKF 的计算复杂度与 EKF 相同。

如前所述，我们将利用 UKF 来更新初始裂纹扩展模型。为此，需要将问题转换为 UKF 框架。需要更新的参数 C 和 m 被视为 UKF 的“状态”。按照惯例，状态用 x 表示。状态被建模为随机游走过程。前面描述的裂纹扩展模型是测量方程。UKF 的过程模型和测量模型一起表示为其中 a 是裂纹尺寸，u 是循环次数，h 表示裂纹扩展模型，w 是过程噪声，v 是测量噪声。过程噪声和测量噪声被假定为零均值、高斯分布和 白噪声。

基于 UKF 的模型更新方法的步骤总结如下

1. 初始化状态向量及其不确定性（协方差）。
   
2. 根据状态生成 sigma 点。
   
3. 传播 sigma 点并计算状态的预测均值和协方差。
   
4. 根据预测的均值和协方差计算 sigma 点。
   
5. 计算每个 sigma 点的输出。
   
6. 计算预测输出，作为步骤 5 中各个输出的加权和。
   
7. 计算预测输出的不确定性（协方差）。
   
8. 计算预测状态和预测输出之间的互协方差。
   
9. 计算创新为测量输出与预测输出之差。
   
10. 使用互协方差和输出协方差计算滤波器增益。
    
11. 更新状态向量及其协方差。
    
12. 对用于模型更新的所有数据点重复步骤 2 到 11。
    

好奇的读者可以了解 UKF 背后的数学原理，这里。

基于 UKF 的裂纹扩展模型更新方法已作为 Depend On Docker 项目实现，可以在此 仓库 中找到，Google Colab 在这里。为了清楚起见，下面提供了一些算法关键步骤的代码片段。

生成 Sigma 点

可以使用以下代码在 TensorFlow 中生成 Sigma 点

## Inputs: State Vector - x_prev, Covariance Matrix - cov_prev, # States - num_st, UKF Parameter - kappa
## Output: Sigma Points Matrix - sig

[eigval, eigvec] = tf.linalg.eigh(cov_prev)                                   # Eigen Decomposition of the covariance matrix        
S_tf = tf.diag(tf.sqrt(eigval))                                               
sqrt_cov = tf.matmul(tf.matmul(eigvec, S_tf), tf.matrix_inverse(eigvec))      # Square-root of the covariance matrix
eta = tf.sqrt((alpha ** 2) * (num_st + kappa))                                # UKF scaling factor
sqrt_sc = tf.scalar_mul(eta, sqrt_cov)                                        # Scaled square-root
sig = np.matlib.repmat(x_prev, 1, 2*num_st+1)
sig[:, 1:num_st+1] = sig[:, 1:num_st+1] + sqrt_sc
sig[:, num_st+1:2*num_st+1] = sig[:, num_st+1:2*num_st+1] - sqrt_sc           # Sigma points

预测均值和协方差

生成 Sigma 点后，它们会通过过程模型进行传播。然后，传播的 Sigma 点用于计算预测的均值和协方差。

## Inputs:  Sigma Point Matrix - sig, UKF Weights - w0_mean, w0_cov, wi, # States - num_st, Process covariance - Q
## Outputs: Predicted State Vector - x_minus, Predicted Covariance - cov_minus

x_minus = w0_mean * sig[:, 0] + w_i * tf.reduce_sum(sig[:, 1:2 * num_st + 1], axis=1)
x_minus = tf.reshape(x_minus, (num_st, 1))
temp1 = tf.reshape(sig[:, 0], (num_st, 1))
# Predict Covariance
cov_minus = w0_cov * (temp1 - x_minus) * tf.transpose((temp1 - x_minus))
for i in range(1, 2 * num_st + 1):
  temp1 = tf.reshape(sig[:, i], (num_st, 1))
  cov_minus = cov_minus + w_i * (temp1 - x_minus) * tf.transpose((temp1 - x_minus))
  cov_minus = cov_minus + Q

计算所有 Sigma 点的输出

所有 Sigma 点的输出计算如下

## Inputs: Sigma Point Matrix - sig, Current Crack Size - init_crack, Stress Constant - dsig,
##         Cycles Interval - diff_cycles, # States - num_st
## Output: Output Matrix - gam

gam = np.zeros((1, 2*num_st+1))
for indx in range(0, 2*num_st+1):
  logC = sig[0, indx]
  m = sig[1, indx]
  gam[:, indx] = predict_crack(diff_cycles, logC, m, init_crack, dsig)

计算输出、互协方差和输出协方差

预测输出、互协方差和输出协方差计算如下

## Inputs:  Output Matrix - gam, Sigma Point Matrix - sig, State Vector - x_prev, UKF Parameters - w0_mean, w0_cov, wi,
##          # States - num_st, Measurement Covariance - R
## Outputs: Cross Covariance - cov_xy, Output Covariance - cov_yy, Output Vector - yhat

yhat = w0_mean * gam[:, 0] + w_i * tf.reduce_sum(gam[:, 1:2 * num_st + 1])            # Output vector
temp2 = tf.reshape(sig[:, 0], (num_st, 1))
cov_yy = w0_cov * (gam[:, 0] - yhat) * tf.transpose(gam[:, 0] - yhat)                 # Output covariance
cov_xy = w0_cov * (temp2 - x_prev) * tf.transpose(gam[:, 0] - yhat)                   # Cross covariance
for i in range(1, 2*num_st+1):
  temp2 = tf.reshape(sig[:, i], (num_st, 1))
  cov_yy = cov_yy + w_i * (gam[:, i] - yhat) * tf.transpose(gam[:, i] - yhat)
  cov_xy = cov_xy + w_i * (temp2 - x_prev) * tf.transpose(gam[:, i] - yhat)

cov_yy = (cov_yy + tf.transpose(cov_yy))/2                                            # Ensure symmetry
cov_yy = cov_yy + R

更新状态向量及其协方差

最后，更新状态向量及其协方差。

## Inputs : Predicted State Vector - x_minus, Predicted State Covariance - cov_minus, Predicted Output - yhat,
#           Measured Output - y, Output Covariance cov_yy, Cross Covariance - cov_xy
## Outputs: Updated State Vector - x_hat, Updated State Covariance - cov_hat

k_gain = cov_xy * np.linalg.inv(np.matrix(cov_yy))                            # calculate filter gain
innov = y - y_hat                                                             # innovation
x_hat = x_minus + k_gain * innov                                              # update state
cov_hat = cov_minus - k_gain * cov_yy * tf.transpose(k_gain)                  # update covariance
cov_hat = (cov_hat + tf.transpose(cov_hat)) / 2                               # ensure symmetry

结果与讨论

如前所述，更新数据集用于使用 UKF 优化初始模型。更新后的模型参数为：logC = -22.2037 & m = 3.5762。模型更新前后的预测结果如下所示： 可以观察到，与初始模型相比，更新后的模型预测更准确。但这只是一个显而易见的结果，因为我们正在对用于更新模型的同一数据集进行预测。只有在使用未用于更新的数据集验证更新后的模型预测时，才能真正衡量更新后的模型的准确性。更重要的是，更新后的模型在预测裂纹的未来演变方面应该比初始模型更准确。否则，即使更新后的模型也并不特别有用。

因此，更新后的模型用于预测对应于测试数据集的循环的裂纹尺寸。更新后的模型预测的裂纹尺寸以及初始模型的裂纹尺寸如下所示： 基于 UKF 的模型更新方法不仅估计模型参数的均值，还计算与估计相关的协方差。换句话说，它提供了状态变量的联合分布。TensorFlow Probability 的 MultivariateNormalFullCovariance 函数用于创建样本，以计算与预测输出（在本例中为裂纹尺寸）相关的 uncertainty。预测裂纹尺寸的 95% 可信区间也绘制在上面的图形中。

从图中可以清楚地看出，与初始模型相比，更新后的模型在预测裂纹的未来演变方面明显更准确。这表明 UKF 能够从更新数据集中的测量值中提取相关信息，以修改模型参数，使模型更准确、更有用。这里要提到的另一个重要事项是这种方法对噪声测量的鲁棒性。在更新数据集中，对应于循环 600 和 700 的测量值与其他测量的裂纹值相比是异常值。但是，这些异常值对模型更新过程的影响相当小，因为 UKF 没有尝试最小化这些数据点上的预测和观察之间的误差。这是一个理想的结果，这种对噪声测量的鲁棒性对于获得准确的更新模型至关重要。

最后，我们使用初始模型和更新后的模型预测裂纹尺寸到 2200 个循环。预测结果以及更新后的模型的 uncertainty 边界如下所示。

从上面的图表中可以明显看出，如果使用初始模型，裂纹预测将非常不准确。实际上，初始模型将在 2100 个循环时产生错误警报，而此时发现大于修复阈值的裂纹的真实概率非常小（<< 5%）。

总结

我们展示了如何解决“已知未知”的问题，正如我们在本博客系列的 第一部分 中所描述的那样。在第一部分中，我们展示了如何结合领域知识和传统 ML 来计算材料属性的已知已知。本博客展示了更现实的设置中的相同示例，其中并非所有数据都预先可用。本博客中讨论的基于 UKF 的预测模型更新方法在数据有限且存在噪声的现实应用中非常有效。它可以适应模型中的非线性，并且计算效率高。

后续步骤

在我们从 第一部分 中的概念的基础上，我们在第二部分中将已知已知问题扩展到了已知未知。下一部分将讨论未知未知的情况，将所有三个部分整合在一起。关于贝叶斯模型选择和模型优化的几个悬而未决的问题将在以后的博客中讨论。

致谢

这篇博客是 Google 和 BHGE 多个团队的辛勤工作和深度合作的结果。我们特别感谢 Josh Dillon、Mike Shwe、Scott Fitzharris、Alex Walker、Shyam Sivaramakrishnan 和 Fabio Nonato 的多次编辑、结果、代码片段以及最重要的热情支持。