作者: Mike Shwe，Google TensorFlow Probability 产品经理；Josh Dillon，Google TensorFlow Probability 软件工程师；Bryan Seybold，Google 软件工程师；Matthew McAteer；以及 Cam Davidson-Pilon。

您是概率编程新手吗？您是 TensorFlow Probability (TFP) 新手吗？那么我们为您准备了一些东西。黑客的贝叶斯方法，一个入门级的动手教程，现在已提供 TFP 示例。TFP 版本作为开源资源供所有人使用，它补充了之前用 PyMC3 编写的版本。

黑客的贝叶斯方法有很多不错的特点：它不仅对概率新手友好，而且还展示了如何将概率编程应用于现实世界的问题。

概率编程，人人可享

虽然贝叶斯方法不是概率编程的必要条件，但它提供了一个直观的框架来表示信念，并根据新数据更新这些信念。黑客的贝叶斯方法以一种动手的方式教授这些技术，使用 TFP 作为底层。由于这本书是用 Google Colab 编写的，您可以运行和修改 Python 示例。

TensorFlow 团队 为希望编码领域知识来理解数据和做出预测的数据科学家、统计学家以及机器学习研究人员和从业者构建了 TFP。TFP 是一个基于 TensorFlow 的 Python 库，它使在现代硬件上轻松地结合概率模型和深度学习成为可能。TFP 允许您

• 探索您的数据
• 评估不同的模型
• 利用现代的矢量化硬件加速器
• 启动轻松自如。TFP 是专业构建和测试的，Google 云就绪，并由一个充满活力的开源社区支持。

正如我们在相关的博客文章中所讨论的，概率编程具有多种应用，包括 金融 和 石油和天然气行业。为什么？不确定性无处不在。现实世界中的现象 - 即使是我们完全理解的现象 - 也受到我们无法控制甚至意识到的外部因素的影响。忽视这些因素意味着结论可能是错误的，或者充其量是误导性的。我们构建 TFP 的目的是让所有人都可以使用它，来模拟我们周围的不确定性。

解决现实世界的问题

许多贝叶斯教程都集中在解决具有解析解的简单问题上：例如抛硬币和掷骰子。虽然黑客的贝叶斯方法从这些问题开始，但它很快转向了更现实的问题。示例范围从了解宇宙到检测在线用户行为的变化。

在本博客的剩余部分，我们将概述一个著名的现实世界问题，它在黑客的贝叶斯方法书中得到了更详细的处理 第 2 章：1986 年的挑战者号航天飞机灾难。

1986 年 1 月 28 日，在美国航天飞机挑战者号的第 25 次飞行中，航天飞机挑战者号上的两个固体火箭助推器之一发生了爆炸，这是由于 O 形圈失效造成的。尽管任务工程师与 O 形圈制造商进行了多次关于之前飞行中损坏情况的沟通，但制造商认为风险是可以接受的 [1]。

下面，我们描述了之前航天飞机任务中七起 O 形圈损坏事件的观测结果，这些结果是作为环境温度的函数。 (在 70 度时，有两次事件。)

您会注意到，随着温度降低，损坏的 O 形圈比例明显增加，但没有明显的温度阈值，低于此阈值，O 形圈可能会失效。与大多数现实世界中的现象一样，也存在不确定性。我们希望确定在给定温度 *t* 时，O 形圈失效的概率是多少？

我们可以使用逻辑函数来模拟温度 *t* 时 O 形圈损坏的概率 *p*，具体来说
其中 β 决定了逻辑函数的形状，而 α 是偏置项，将函数从左向右移动。由于这两个参数都可以是正数或负数，并且在大小上没有特定限制或偏差，我们可以将它们建模为高斯随机变量
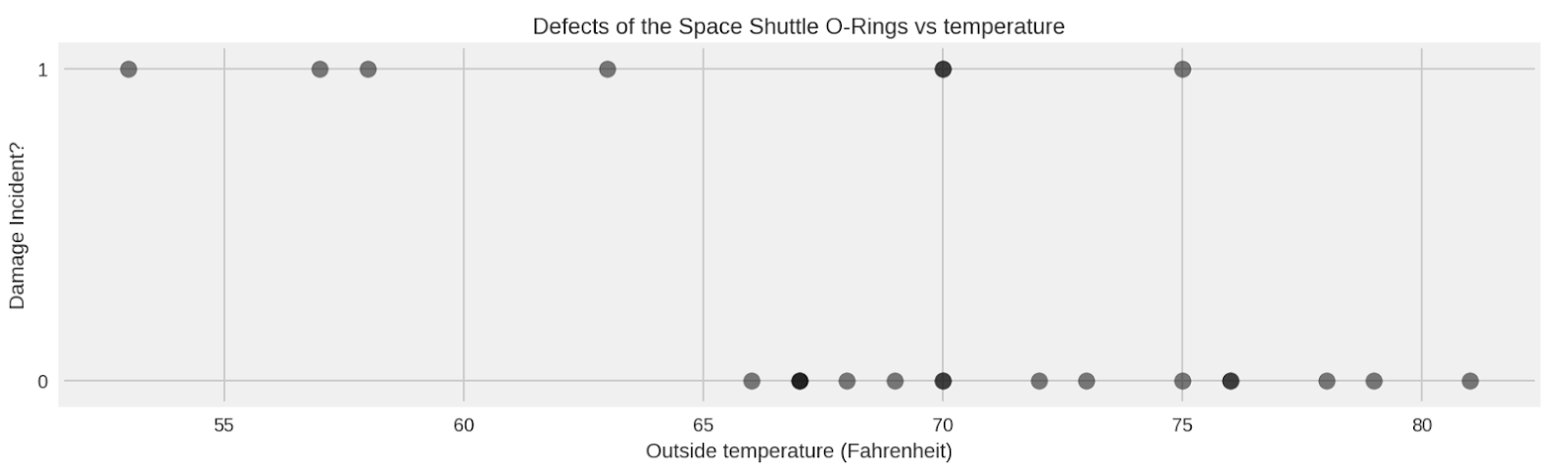
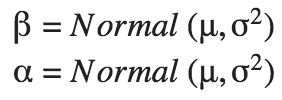
在 TFP 中，我们可以直观地使用 tfp.distributions.Normal 来表示 α 和 β，如以下代码片段所示

temperature_ = challenger_data_[:, 0]
temperature = tf.convert_to_tensor(temperature_, dtype=tf.float32)
D_ = challenger_data_[:, 1]                # defect or not?
D = tf.convert_to_tensor(D_, dtype=tf.float32)

beta = tfd.Normal(name="beta", loc=0.3, scale=1000.).sample()
alpha = tfd.Normal(name="alpha", loc=-15., scale=1000.).sample()
p_deterministic = tfd.Deterministic(name="p", loc=1.0/(1. + tf.exp(beta * temperature_ + alpha))).sample()

[
    prior_alpha_,
    prior_beta_,
    p_deterministic_,
    D_,
] = evaluate([
    alpha,
    beta,
    p_deterministic,
    D,
])

(要运行此代码片段，请前往 第 2 章的 Google Colab 版本，这样您就可以运行整个航天飞机示例)。

请注意，我们在第 8 行获得 *p*(t) 的实际值 0 或 1，在该行中，我们使用第 6 行和第 7 行中先前采样的 α 和 β 值从逻辑函数中进行采样。此外，请注意，evaluate() 辅助函数允许我们在图形模式和急切模式之间无缝切换，同时将张量值转换为 numpy。我们在 第 2 章 的开头更详细地描述了急切模式和图形模式以及此辅助函数。

要将温度 *t* 时失效的概率 *p(t)* 与我们的观测数据联系起来，我们可以使用参数为 *p(t)* 的伯努利随机变量。请注意，一般来说，*Ber(p)* 是一个随机变量，它以概率 *p* 取值 1，否则取值 0。因此，我们生成模型的最后部分是，我们在温度值 *i* 处有一个缺陷事件 *D*𝑖，它可以建模为
鉴于这个生成模型，我们希望找到模型参数，以便模型可以解释我们的观测数据 - 这就是概率推理的目标！

TFP 通过使用未归一化的联合对数概率函数来评估模型，从而执行概率推理。此 joint_log_prob 的参数是数据和模型状态。该函数返回参数化模型生成观测数据的联合概率的对数。要详细了解 joint_log_prob，请参阅 此说明。

为了说明挑战者号示例，以下是如何定义 joint_log_prob

def challenger_joint_log_prob(D, temperature_, alpha, beta):
    """
    Joint log probability optimization function.
        
    Args:
      D: The Data from the challenger disaster representing presence or 
         absence of defect
      temperature_: The Data from the challenger disaster, specifically the temperature on 
         the days of the observation of the presence or absence of a defect
      alpha: one of the inputs of the HMC
      beta: one of the inputs of the HMC
    Returns: 
      Joint log probability optimization function.
    """
    rv_alpha = tfd.Normal(loc=0., scale=1000.)
    rv_beta = tfd.Normal(loc=0., scale=1000.)
    logistic_p = 1.0/(1. + tf.exp(beta * tf.to_float(temperature_) + alpha))
    rv_observed = tfd.Bernoulli(probs=logistic_p)
  
    return (
        rv_alpha.log_prob(alpha)
        + rv_beta.log_prob(beta)
        + tf.reduce_sum(rv_observed.log_prob(D))
    )

请注意，第 15-18 行简洁地编码了我们的生成模型，每个随机变量一行。此外，请注意，rv_alpha 和 rv_beta 代表我们对 α 和 β 的先验分布的随机变量。相比之下，rv_observed 代表给定由 α 和 β 参数化的逻辑分布时，温度和 O 形圈结果中观测结果的似然的条件分布。

接下来，我们将 joint_log_prob 函数发送到 tfp.mcmc 模块。马尔可夫链蒙特卡洛 (MCMC) 算法对未知输入值进行有根据的猜测，计算 joint_log_prob 函数中参数集的可能性。通过多次重复此过程，MCMC 构建了可能参数的分布。构建此分布是概率推理的目标。

因此，我们将设置一种特定类型的 MCMC，称为 哈密顿蒙特卡洛，在我们的 challenge_joint_log_prob 函数上

number_of_steps = 10000
burnin = 2000

# Set the chain's start state.
initial_chain_state = [
    0. * tf.ones([], dtype=tf.float32, name="init_alpha"),
    0. * tf.ones([], dtype=tf.float32, name="init_beta")
]

# Since HMC operates over unconstrained space, we need to transform the
# samples so they live in real-space.
# Alpha is 100x of beta approximately, so apply Affine scalar bijector
# to multiply the unconstrained alpha by 100 to get back to 
# the Challenger problem space
unconstraining_bijectors = [
    tfp.bijectors.AffineScalar(100.),
    tfp.bijectors.Identity()
]

# Define a closure over our joint_log_prob.
unnormalized_posterior_log_prob = lambda *args: challenger_joint_log_prob(D, temperature_, *args)

# Initialize the step_size. (It will be automatically adapted.)
with tf.variable_scope(tf.get_variable_scope(), reuse=tf.AUTO_REUSE):
    step_size = tf.get_variable(
        name='step_size',
        initializer=tf.constant(0.5, dtype=tf.float32),
        trainable=False,
        use_resource=True
    )

# Defining the HMC
hmc=tfp.mcmc.TransformedTransitionKernel(
    inner_kernel=tfp.mcmc.HamiltonianMonteCarlo(
        target_log_prob_fn=unnormalized_posterior_log_prob,
        num_leapfrog_steps=40, #to improve convergence
        step_size=step_size,
        step_size_update_fn=tfp.mcmc.make_simple_step_size_update_policy(
            num_adaptation_steps=int(burnin * 0.8)),
        state_gradients_are_stopped=True),
    bijector=unconstraining_bijectors)

# Sampling from the chain.
[
    posterior_alpha,
    posterior_beta
], kernel_results = tfp.mcmc.sample_chain(
    num_results = number_of_steps,
    num_burnin_steps = burnin,
    current_state=initial_chain_state,
    kernel=hmc)

# Initialize any created variables for preconditions
init_g = tf.global_variables_initializer()

最后，我们将通过 evaluate() 辅助函数实际执行推理

evaluate(init_g)
[
    posterior_alpha_,
    posterior_beta_,
    kernel_results_
] = evaluate([
    posterior_alpha,
    posterior_beta,
    kernel_results
])
    
print("acceptance rate: {}".format(
    kernel_results_.inner_results.is_accepted.mean()))
print("final step size: {}".format(
    kernel_results_.inner_results.extra.step_size_assign[-100:].mean()))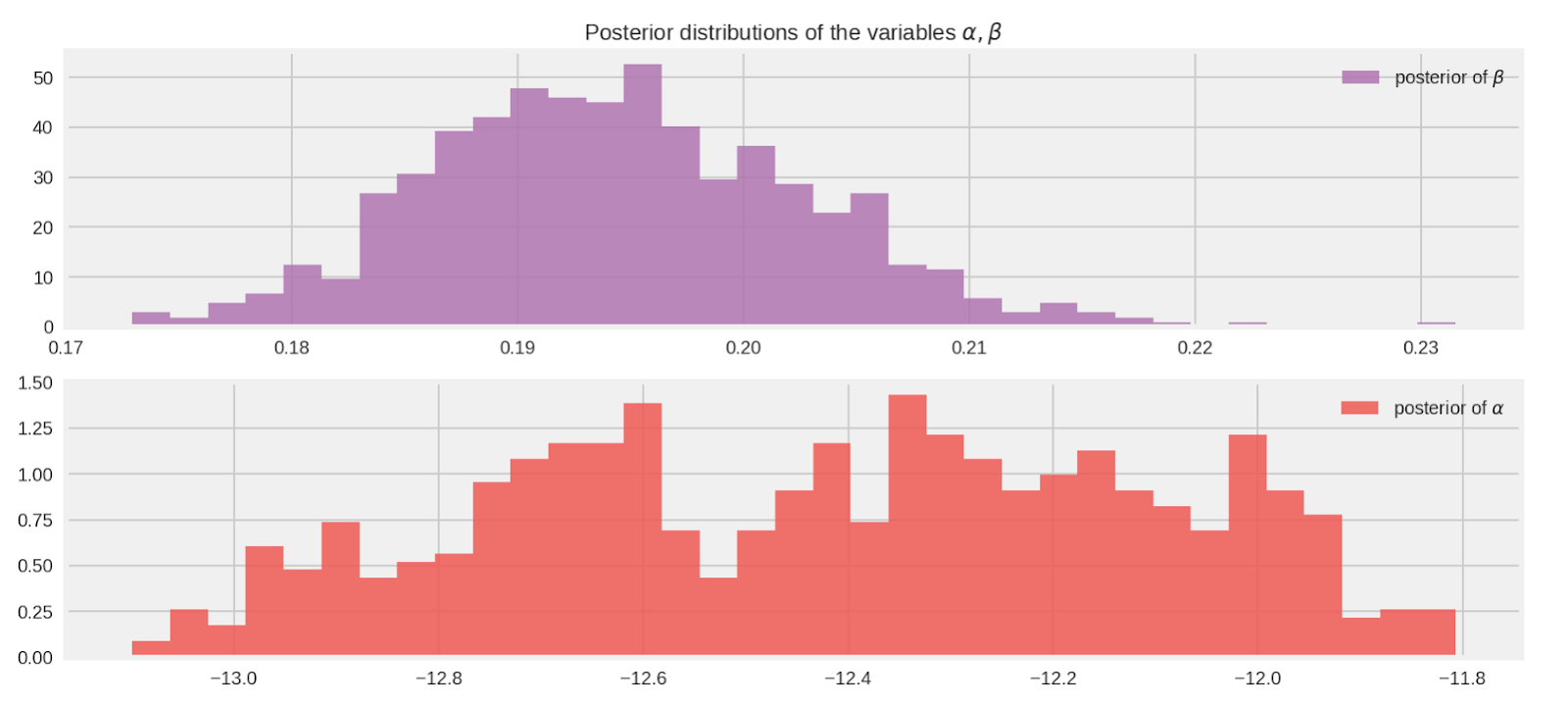

绘制 α 和 β 的分布，我们注意到分布相当宽，正如人们对如此少的样本点和失效和非失效观测之间温度重叠所预料的那样。然而，即使分布很宽，我们也可以相当肯定温度确实对 O 形圈损坏的概率有影响，因为 β 的所有样本都大于 0。我们同样可以确定 α 显着小于 0，因为所有样本都远小于 0。

如上所述，我们真正想知道的是：*在给定温度下，O 形圈损坏的预期概率是多少？* 要计算此概率，我们可以对后验的所有样本进行平均，以获得 *p(t𝑖)* 的可能值。

alpha_samples_1d_ = posterior_alpha_[:, None]  # best to make them 1d
beta_samples_1d_ = posterior_beta_[:, None]

beta_mean = tf.reduce_mean(beta_samples_1d_.T[0])
alpha_mean = tf.reduce_mean(alpha_samples_1d_.T[0])
[ beta_mean_, alpha_mean_ ] = evaluate([ beta_mean, alpha_mean ])

print("beta mean:", beta_mean_)
print("alpha mean:", alpha_mean_)
def logistic(x, beta, alpha=0):
    """
    Logistic function with alpha and beta.
        
    Args:
      x: independent variable
      beta: beta term 
      alpha: alpha term
    Returns: 
      Logistic function
    """
    return 1.0 / (1.0 + tf.exp((beta * x) + alpha))

t_ = np.linspace(temperature_.min() - 5, temperature_.max() + 5, 2500)[:, None]
p_t = logistic(t_.T, beta_samples_1d_, alpha_samples_1d_)
mean_prob_t = logistic(t_.T, beta_mean_, alpha_mean_)
[ 
    p_t_, mean_prob_t_
] = evaluate([ 
    p_t, mean_prob_t
])

然后，我们可以计算出整个温度范围内的 95% 可信区间。请注意，这是一个*可信区间*，而不是通常在频率统计分析方法中找到的*置信区间*。95% 的可信区间告诉我们，我们可以 95% 确定真值将位于该区间内。例如，正如我们使用紫色区域所示，在 50 度时，我们可以 95% 确定失效的概率介于 1.0 和 0.80 之间。具有讽刺意味的是，许多人错误地将置信区间解释为具有此属性。

在挑战者号灾难发生的那天，在 31 度时，事实证明，O 形圈失效的后验分布将使我们得出结论：我们可以高度相信会发生问题。

这个相当直接的概率分析证明了 TFP 和贝叶斯方法的强大功能：它们可用于提供对具有重大影响的现实世界问题的宝贵见解和预测。

继续阅读！

您将在贝叶斯黑客书中找到大量现实世界的例子。您可以将短信量的分析应用于制造和生产系统中各种各样的故障检测问题。谷歌的软件工程师将短信分析方法应用于生产软件的文本不稳定性理解 - 在我们首次起草 TFP 版本的章节后几周内。

您还将找到一种分析方法来查找宇宙中的暗物质。此外，还有预测上市公司股票的回报，即股票收益。

我们希望您能深入研究书中的概念性演练，将这些技术应用于您所在领域的问题。请在github中发表评论和请求，帮助我们保持本书的最佳状态！

致谢

感谢TensorFlow Probability 团队在编写贝叶斯黑客书籍的 TFP 版本时提供的帮助。

参考文献

[1] https://en.wikipedia.org/wiki/Space_Shuttle_Challenger_disaster